Dear Andreas,
yes, indeed we already had a short contact some times ago.
My current approach is to have one source file and handle
compiler specific stuff with a preprocessor (e.g. the "convenient"
EXPORT clauses in XDS Modula). In some rare cases I also have 2
implementation modules fitting to one definition module - but that
should be an exception as the code then quickly becomes
unmaintainable in my personal view. But that might be different if
done in a team ...
A x V = \lambda V
=> V^{tr} x A x V - \lambda = residual (should be zero in
exact arithmetic)
the residual is not more than a small times the machine precision (or whatever is appropriate).
As already said, the library grow around my personal needs over a
long period - I do not have the intend to make it replace packages
such as Lapack / GSL or others. It would be great if someone finds
parts useful for her/his purpose, that's all.
But if you have some hints how you and your team are doing tests
and handle different compilers/hardware it would be highly
appreciated to get into touch.
At the moment I am especially struggling with the "unusual"
definition of LONGREAL in GM2 with 12 bytes as that does not match
with Fortran's "REAL (kind=8)" (old "DOUBLE PRECISION") or "C"
double. I could think to define a type e.g. "FLOAT" that is "REAL"
for GM2 and "LONGREAL" for other compilers, but that does not
circumvent issues with the import of libraries (LongMath versus
RealMath just as an minor example). Any hint how that can be
handled would be welcome - I saw that had been discussed years ago
before I got in touch with GM2 ...
Michael
Dear Michael,
I guess I already contacted you once on our test suite we developed while developing RAMSES.
However, for numerics to work well, integer arithmetic needs to be considered as well. Our numerics test programs test therefore not only real, but also integer arithmetic for single and double precision, notably for conforming to IEEE floating point standards.
Moreover, the design of math libs is not without issues whatever your approach, in particular not trivial if your aim is to obtain a portable version (our case where RAMSES should give you identical results regardless of the hardware or OS).
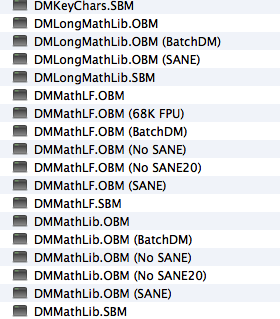
Unfortunately, our design – I would be happy to share with you – is rather complex for many reasons (ease of maintenance, portability, use of several compilers, use of several libraries). As one consequence we are using several implementation variants for many modules that interface with the underlying system, including real arithmetic modules, while keeping a simple common basis of as few non-portable modules as possible. This approach has evolved due to the need to obtain identical results on several platforms. Since we nevertheless tried to make good use of existing approaches, e.g. a well tested C library, we needed also the flexibility to switch between our own BatchDM variant and some external approach, may that be provided via hardware (e.g. math (co-)processor) or via software (e.g. the aforementioned C library). A typical release of the RAMSES libraries contains then several implementation variants of the very same module that need to be made available for the linker via renaming of the object file. Here some illustrative examples:
All these variants having different efficiency and numerics. To keep things as portable as possible we use for real arithmetics FloatPortab, our own implementation of the IEEE floating point standard.
To make sure during each release that all numerics work reliably, we have developed test suites that check many properties of the resulting arithmetic, including NAN operations.
None of these modules would work right away in another environment, since aforementioned variants depend on compiler and/or platform, thus the actual code of these modules is automatically switched by a few global flags using scripts contained in our release machinery. Yet, perhaps one or the other element might be of interest.
Let me know whether you are interested or not.
Regards,Andreas
P.S.: BTW SANE stands for Standard Apple Numerics Environment, available on many Apple machines since Apple II, which was an excellent and very strict implementation of theIEEE floating point standard. Unfortunately Apple has given up on SANE. We still support it mostly.
ETH Zurich
Prof. em. Dr. Andreas Fischlin
IPCC Vice-Chair WGII
Systems Ecology - Institute of Biogeochemistry and Pollutant Dynamics
Universitaetstrasse 16, CHN E 24
8092 Zurich
SWITZERLAND
address@hidden
www.sysecol.ethz.ch/people/andreas.fischlin.html
+41 44 633-6090 phone
+41 79 595-4050 mobile
Make it as simple as possible, but distrust it!
________________________________________________________________________
On 03/06/2018, at 12:51, Michael Riedl <address@hidden> wrote:
Hallo all,
just as an info - I am still working on my libraries to get them in a
state to go into the public.
Currently I am collecting all test cases in a (more or less) systematic
way to get all in the
position to check if a compiled version works as it should - still a
long way to go ;-)
I am now making myself familiar with GIT and placed the source files to
https://opensourceprojects.eu/p/modula2/wiki/Home/
in two folders (Inout & Numerik). Will add the test code step by step ...
Would be kind if someone can provide me with a feedback it the files are
accessible not only for me ...
Thanks
Michael
PS: The filing location might be changed in the future, at the moment I
just want to ensure that the files
are not only on my personal equipment and get familiar with the git tool ...
_______________________________________________
gm2 mailing list
address@hidden
https://lists.nongnu.org/mailman/listinfo/gm2