Re: [Groff] Problems with arcs and angles

[John Gardner]

Looks like there's a mistake in groff_out(5). It describes its arc-drawing
command as:

*Draw arc from current position to (h1, v1)+(h2, v2) with center at (h1,
> v1);*


However, gropdf.pl tells a different story. To quote line #2791:
<http://git.savannah.gnu.org/cgit/groff.git/tree/src/devices/gropdf/gropdf.pl?id=453a8aa7c8f8dd0c78160466301f81be8c40df2e#n2791>

*Documentation is wrong. Groff does not use Dh1,Dv1 as centre of the
> circle!*


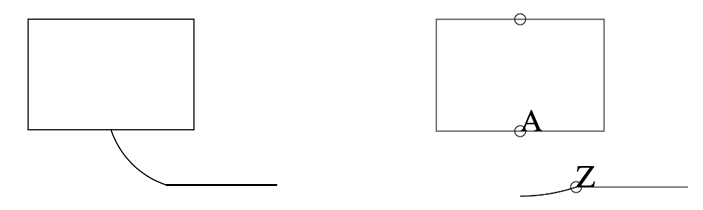
I noticed something odd when drawing an arc which wasn't an evenly-sized
quarter-circle. For instance, the following Pic code:

.PS
> move down
> A: box
> arc at A.n
> line right
> .PE


... generates the following output:


> …

V84000

H99000
> Da 0 -36000 18000 54000


Which looks like this in gropdf and my own canvas code, respectively:

[image: Inline images 3]
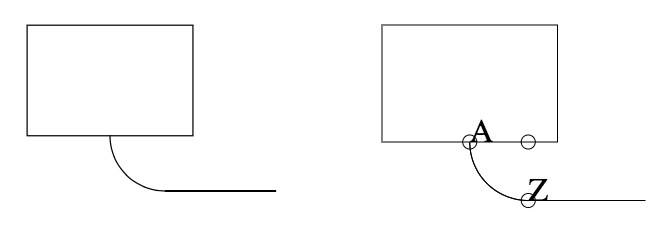
I've marked the start (A) and end (Z) points in my output on the right. The
circle at the top denotes where the centre-point is. Compare that with an
ordinary arc (e.g., replace `arc at A.n` in the previous Pic code with `arc`
instead):

[image: Inline images 5]
gropdf is also drawing each arc in 4 segments, instead of 1. The reasons
why are unclear to me.

Otherwise, I've succeeded in drawing every other (quartercircle-sized) arc
using the following code:

centreX    = h1 + startX
> centreY    = v1 + startY
> endX       = centreX + h2
> endY       = centreY + v2
> radius     = sqrt(pow(endX - centreX, 2) + pow(endY - centreY, 2))
> startAngle = atan2(startY - centreY, startX - centreX)
> endAngle   = atan2(endY   - centreY, endX   - centreX)




On 30 April 2017 at 20:18, John Gardner <address@hidden> wrote:

> Sorry for the delayed response. Some pull-requests needed tending to
> before I had a chance to go through all this.
>
> First, thank you all so much for your help and patience! It truly means a
> lot. I've not yet got arcs drawing correctly, but I feel I'm coming close.
> Branden's pointers on trigonometry cleared some cobwebs that hadn't been
> lifted since high-school trigonometry lessons, making all this slightly
> easier to follow.
>
> Turns out the HTML5 specification
> <https://html.spec.whatwg.org/multipage/scripting.html#dom-context-2d-arc> 
> itself
> offers a much clearer description of arc-drawing than the docs I linked to
> earlier:
>
>
>> *Consider an ellipse that has its origin at (x, y), that has a major-axis
>> radius radiusX and a minor-axis radius radiusY, and that is rotated about
>> its origin such that its semi-major axis is inclined rotation radians
>> clockwise from the x-axis.*
>
>
>> *If anticlockwise is false and endAngle-startAngle is equal to or greater
>> than 2π, or, if anticlockwise is true and startAngle-endAngle is equal to
>> or greater than 2π, then the arc is the whole circumference of this
>> ellipse, and the point at startAngle along this circle's circumference,
>> measured in radians clockwise from the ellipse's semi-major axis, acts as
>> both the start point and the end point.*
>
>
>
> *Otherwise, the points at startAngle and endAngle along this circle's
>> circumference, measured in radians clockwise from the ellipse's semi-major
>> axis, are the start and end points respectively, and the arc is the path
>> along the circumference of this ellipse from the start point to the end
>> point, going anti-clockwise if anticlockwise is true, and clockwise
>> otherwise. Since the points are on the ellipse, as opposed to being simply
>> angles from zero, the arc can never cover an angle greater than 2π radians.*
>
>
> It also explains how arcs and ellipses are drawn using the same
> coordinates:
>
> *The arc() method is equivalent to the ellipse() method in the case where
>> the two radii are equal. When the arc() method is invoked, it must act as
>> if the ellipse() method had been invoked with the radiusX and radiusY
>> arguments set to the value of the radius argument, the rotation argument
>> set to zero, and the other arguments set to the same values as their
>> identically named arguments on the arc() method.*
>
>
> Going forward, I *think* I can work this out.
>
> I hope B-spline drawing doesn't turn out to be as difficult. =(
>
> Thank you all again!
>
>
>
> On 29 April 2017 at 01:38, Ralph Corderoy <address@hidden> wrote:
>
>> Hi John,
>>
>> > <https://cdn.rawgit.com/Alhadis/language-roff/a7c07744a9d44a
>> df32a546646f7a8d57d52e6e58/preview-tty.html>
>> > <https://cloud.githubusercontent.com/assets/2346707/
>> 25514878/732e09ea-2c23-11e7-97ea-9674d3845dd1.png>
>>
>> Gorgeous.  :-)
>>
>> > Groff's output gives me these coordinates to go by:
>> >
>> >    - startX, startY - Coordinates of the arc's starting point
>> >    - centreX, centreY - Coordinates of the arc's centre
>> >    - endX, endY - Coordinates of the arc's terminal point
>>
>> I'm assuming centreX and centreY are zero as it's just a simple
>> translation to get there.  And for the moment that startX and startY are
>> in the x>0, y>0 quadrant.  This gives a right-angled triangle (0, 0),
>> (startX, 0), (startX, startY).
>>
>> > But the canvas arc method I'm working with requires all of these:
>> >
>> >    - x - The x coordinate of the arc's centre.
>> >    - y - The y coordinate of the arc's centre.
>>
>> 0, 0.
>>
>> >    - radius - The arc's radius.
>>
>> sqrt(startX**2, startY**2) as pic's arcs are always circular.
>>
>> >    - startAngle - The angle at which the arc starts, measured clockwise
>> >    from the positive x axis and expressed in radians.
>>
>> That's the triangle's angle at its origin corner.  That's the arc sine
>> of the opposite edge's length, startY.  But this assumes the radius,
>> i.e. triangle's hypotenuse, is 1.  When it's not, it's
>> asin(startY/radius).
>>
>> This bit of Python might help.
>>
>>     >>> from math import *
>>     >>> def d(r): return r / pi * 180
>>     ...
>>     >>> d(asin(0.001))
>>     0.05729578906238321
>>     >>> d(asin(0.999))
>>     87.43744126687686
>>     >>>
>>     >>> d(asin(1))
>>     90.0
>>     >>> d(asin(-1))
>>     -90.0
>>     >>>
>>     >>> d(asin(-0.001))
>>     -0.05729578906238321
>>     >>> d(asin(-0.999))
>>     -87.43744126687686
>>     >>>
>>     >>> d(asin(0.5))
>>     30.000000000000004
>>     >>> d(asin(sqrt(0.75)))
>>     60.0
>>
>> You can see asin copes with [1, -1], giving [90, -90] in degrees.
>> You'll need to check the signs of start{X,Y}, making π/2 adjustments to
>> the radians you obtain to handle the other quadrants.
>>
>> Hope that helps.  It's been many decades since I needed this.  :-)
>>
>> --
>> Cheers, Ralph.
>> https://plus.google.com/+RalphCorderoy
>>
>>
>