Le sam. 7 mai 2022 à 14:05, Konstantinos Poulios <logari81@googlemail.com> a écrit :
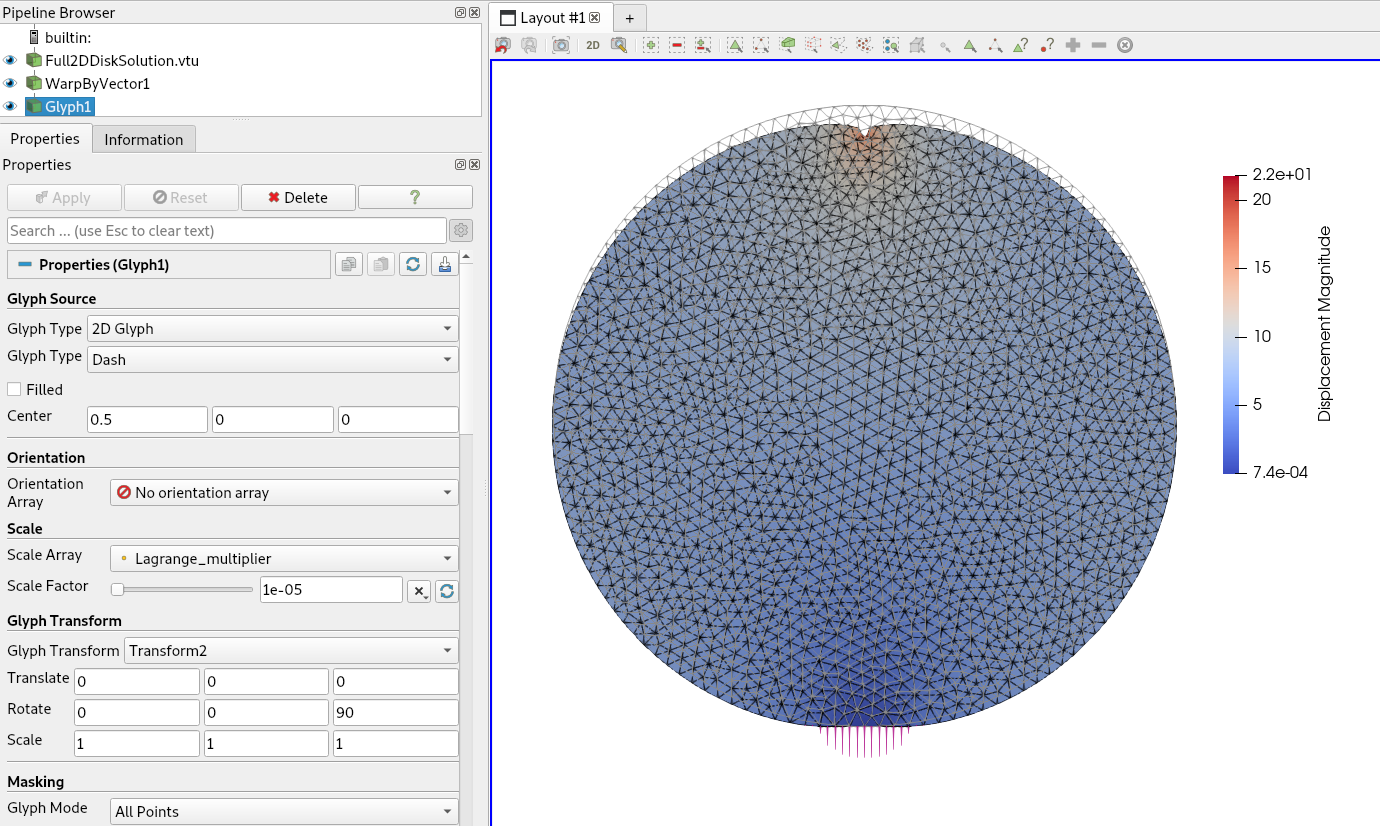
Dear David,There are a few points to clarify1) Regarding the difference of 1st PK traction versus Cauchy traction, your result does not let conclude that is negligible. In fact it looks similar at the top, to the deviation that you showed before.We will need you to show us a much finer resolution and a valid comparison with the analytical Hertzian pressure curve in order to conclude about this point2) The last comparison you showed us cannot be valid because the total load of the analytical result is much lower than the total load in the numerical result. So you need to fix that first.3) The result you showed is very coarse, either your load is too little all the mesh size too large.4) Regarding the quote from our paper. It makes sense, it says that in general for a very large contact width you should not expect the Hertzian solution to be valid, as Andriy basically pointed out. Moreover, for large contact width, the real pressure distribution will depend on the constitutive law. Only if you use the same hyperelastic law that we used in our example 1, you will get a pressure distribution that is quite close to Hertzian, but how close, I cannot tell you. We do not have any very fine comparison in the paper. And it is actually not so interesting either since the result is anyway material-dependent.Best regardsKostasOn Fri, May 6, 2022 at 7:59 PM David Danan <daviddanan9021@gmail.com> wrote:Dear all,Following your suggestions, please find enclosed the deformed disk result and the comparison between the analytical solution (max displacement is small compared to the disk radius=200), the original multiplier and the multiplier converted.I have refined the mesh a bit near the interface to have more points in contact.I had also checked beforehand the value of " (Det(F)*Norm(Inv(F)'*Normal)) " at the contact boundary Gauss points and it was close to 1 everywhere (which was expected in the small deformation theory). Thus, the multiplier and the multiplier converted are almost the same.The "converted multiplier" is interpolated on the nodes with the following commands, where lambda is the contact multipliermflambda=model.mesh_fem_of_variable('lambda')refIndices=mflambda.basic_dof_on_region(boundaryTags["CONTACT_BOUNDARY"])nodesOnContactBoundary=mflambda.basic_dof_nodes().T[refIndices]gwflMult = "lambda/(Det(Id(2)+Grad_u)*Norm(Inv(Id(2)+Grad_u)'*Normal))"newContactMult=model.interpolation(gwflMult, np.transpose(nodesOnContactBoundary), mesh, boundaryTags["CONTACT_BOUNDARY"])Also, even if the results were any different, quoting your 2015 article" It should be noted that the studied problem is not strictly a
Hertzian contact due to the high load resulting to a contact width of considerable size compared
to the disc radius. However, numerical experiments showed that the considered material law (35)
preserves the validity of the Hertzian solution in the finite strain regime quite accurately"Very strange...BR,David.Le ven. 6 mai 2022 à 15:55, Konstantinos Poulios <logari81@googlemail.com> a écrit :Dear Andriy,Yes I agree this is another possible explanation. Basically when the ratio between contact width and contact radius becomes large, the Hertzian solution is not valid anymore. I had somehow assumed that David's plot was for a reasonably small contact width, but you are of course right one should also check that.BRKostasOn Fri, May 6, 2022 at 12:53 PM Andriy Andreykiv <andriy.andreykiv@gmail.com> wrote:Kostas, is it correct to differentiate between 1st Piola Kirchhoff stress and Cauchy stress when we are within small deformation theory?I suspect that when the strains in the David's simulation become large, Hertz analytical solution doesn't apply anymore because of small deformation assumption in Hertz contactOn Fri, 6 May 2022 at 12:20, Konstantinos Poulios via <getfem-users@nongnu.org> wrote:ah ok, I think I know what the issue is here. The Lagrange multiplier for imposing the contact condition corresponds to a 1st Piola Kirchhoff stress, while the analytical solution gives you the Cauchy stress. You can use Nanson's formula to convert between the two. In your model the Lagrange multiplier is like q in the upper left case of the following table:to convert this q to the equivalent one for the upper right case you need to postprocess your Lagrange multiplier and export the following quantity instead:"contact_mult/(Det(F)*Norm(Inv(F)'*Normal))"I hope it works.It is actually a good observation. I don't recall accounting for this difference in the presentation of the results in our paper from 2015, but maybe our meshes were too coarse to notice the difference, compared to your simulations.BRKostasOn Fri, May 6, 2022 at 11:52 AM David Danan <daviddanan9021@gmail.com> wrote:Dear Kostas,first, thank a lot for the feedback, the convergence is much cleaner now!Thanks also for sharing this script here, it contains several features i had never use so far, it's quite interesting/intriguing.However, i am afraid i did not properly explained what my issue was.Somehow, i was able to make the solver converge even without enabling some options for the solve and the result was qualitatively correct, as far as i could tell.But it turned out there is a large difference between the pressure predicted by the Hertz theory and the result i get and i was wondering whether i am doing something wrong. I tried to list the potential suspects in the first emailRegarding your remarks:-Yes,using a punctual load bother me a lot, which is why i wonder if i am supposed to do that to reproduce Hertz analytical case.-Regarding the unit, i wanted to stay in the small deformation assumption as i was not sure the analytical solution is supposed to hold for large deformation. Therefore, here, the Saint Venant Kirchhoff "becomes" a mere Hooke's law.Do you have any idea how to reproduce the analytical results?Thanks to your help regarding the parameters fiddling, i was at least able to reproduce a different case where there is no ponctual force (surfacic load instead) with a half-disk and a different analytical formula and...It worked (see the results enclosed for the pressure comparison on the contact boundary)!Before, it failed to converge. However, this formula is not really well documented at all, i would rather have a comparison with the classical formula.Thanks in advance for your help,David.PS: sorry for the duplicate, i forgot to put the mailing list in copy previouslyLe ven. 6 mai 2022 à 09:23, Konstantinos Poulios <logari81@googlemail.com> a écrit :Dear David,With the attached script you should also be able to reproduce the results for the first example of our paper
https://www.sciencedirect.com/science/article/pii/S0045794915000656(the script is only slightly modified compared to the original one, so that it can run on python3 and the current version of GetFEM).Best regardsKonstantinosOn Fri, May 6, 2022 at 8:45 AM Konstantinos Poulios <logari81@googlemail.com> wrote:Hi,Your script looks very nice and clean. It just needs a bit of fiddling with the augmentation parameter and the solver. The attached version produces this resultJust some general comments:- Point constraints/loads make almost never sense (unless you know beforehand the reaction force at a constrained point will be zero)- Maybe there is some issue with your units, I needed to increase the load to a very large value to get some visible deformations- The Saint-Venant Kirchhoff material law, that we often use for demonstrations, is a "toy" material law. If you do anything with moderate/large strains, use some proper hyperelastic law- The augmentation parameter should be in the same order of magnitude like the modulus of elasticity, from 1-2 orders of magnitude below to 1-2 orders of magnitude above.Best regardsKostasOn Thu, May 5, 2022 at 8:04 PM David Danan <daviddanan9021@gmail.com> wrote:Dear Getfem-users,My issue might be utterly simple, but i cannot find what i am doing wrong...I am trying to compare the solution provided by Getfem to the analytical solution of an Hertzian contact in 2D (namely, a deformable ball against a perfectly rigid plane) but, so far, i do not get correct results.Please, find enclosed my script. I use gmsh python api to generate the mesh but, if you do not want to use it, you can comment the line to generate the mesh in the script and juste use the mesh also enclosed.Here are some of my concerns:-Are the formula used in the script for the analytical contact pressure/contact surface area etc... correct in 2D?-Is it correct to use a punctual nodal force in such a case? Does it make sense in this context?-Is it correct to compare the analytical pressure to the lagrange multipliers?I have also tried to use a testcase provided in Code_Aster documentation and i got much better results, although not perfect but within the tolerance given in the documentation below.
https://www.code-aster.org/doc/default/en/man_v/v1/v1.01.246.pdfIt might be because these formula are for 3D only but i am not sure yet.Thanks in advance for your help,kind regards,David.